In this activity we will investigate the extent to which various polygons tessellate; that is, how they can be used to cover a plane surface without leaving any gaps.
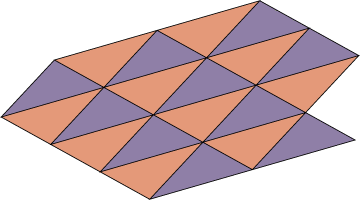
Any triangle may be used to make a tessellation. There are two different tessellations that can be made. The first type is constructed by rotating a copy of the triangle around the center of a side of the original. This tessellation is shown below. Use a triangle tracer and a sheet of paper to form a tessellation using this technique.

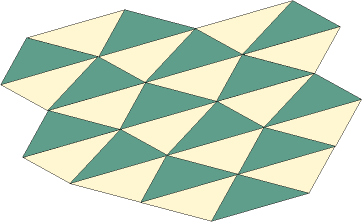
The second type of tessellation for triangles involves reflecting the triangle is a line that includes one of its sides. This tessellation appears below. Use the same triangle tracer to form a tessellation of this type.
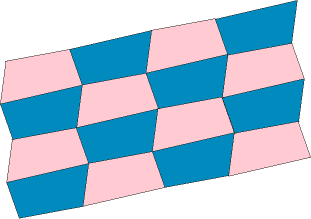
All quadrilaterals will tessellate using the same technique. A copy of the quadrilateral is rotated about the midpoint of a side of the original quadrilateral. An example is shown below. Use a quadrilateral tracer to form a tessellation using this technique.
A regular tessellation is a tessellation of regular polygons with the same code at each vertex. The code for a tessellation can be found by listing the number of sides of each polygon that touches the vertex. This listing is done in order around the vertex. There are only three regular tessellations. The table below shows the measure of each angle of regular polygons with 3 to 12 sides.
| Sides of Polygon | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| Each Angle | 60 | 90 | 108 | 120 | 128 | 135 | 140 | 144 | 147 | 150 |
Since the regular polygons will need to fit together with their angles adjacent to each other around a point, the measure of each angle will need to be a factor of 360°. The only regular polygons that qualify are the equilateral triangle, the square, and the regular hexagon. These tessellations with codes 3-3-3-3-3-3, 4-4-4-4, and 6-6-6, are shown below.



A semi-regular tessellation is a tessellation that is composed of two or more regular polygons with the same code at each vertex. The table on the previous page can be used to find collections of angles of regular polygons that will add up to 360°. Since the smallest angle possible is 60° for the equilateral triangle, there can be no more than 5 regular polygons arranged around a vertex of the tessellation. Moreover, it would not be possible to have less than three regular polygons at a vertex of the tessellation. Find the possible combinations of angles that can be used to make semi-regular tessellations.
____________ ____________ ____________ ____________
____________ ____________ ____________ ____________
____________ ____________ ____________ ____________
____________ ____________ ____________ ____________
____________ ____________ ____________ ____________
____________ ____________ ____________ ____________
The possible combinations of angles will need to be tested to see if a tessellation can actually be formed. When it has been established that the combination produces an actual tessellation, write the code in the space below.
____________ ____________ ____________
____________ ____________
____________ ____________ ____________
Each of the eight semi-regular tessellations can be drawn using a tessellation tracer. Construct at least half of a page with each semi-regular tessellation.
The dual of a tessellation is formed by connect the centers of the shapes in a tessellation so that these segments do not pass through a vertex of the tessellation. The dual tessellations of the regular tessellations are themselves regular tessellations. However, the duals of the semi-regular tessellations are not semi-regular tessellations. Use copies of the semi-regular tessellations to find the dual of each and describe the figure that tessellates in the dual tessellation. Use a code to describe the semi-regular, and the name of a shape to describe the dual.
| Semi-Regular Tessellation | Dual Tessellation |
| ____________________ | ____________________ |
| ____________________ | ____________________ |
| ____________________ | ____________________ |
| ____________________ | ____________________ |
| ____________________ | ____________________ |
| ____________________ | ____________________ |
| ____________________ | ____________________ |
| ____________________ | ____________________ |
A demi-regular tessellation is a tessellation composed of regular polygons with more than two different vertex codes arranged in a repeating pattern. There are an infinite number of possible demi-regular tessellations. Use a tessellation tracer to construct each of the following common demi-regular tessellations, given the vertex code.
| 3-6-3-6 and 3-3-6-6 | 3-12-12 and 3-4-3-12 |
| 3-4-6-4 and 3-4-4-6 | 3-3-3-3-3-3 and 3-3-4-12 |
| 3-4-6-4 and 4-6-12 | 3-3-4-3-4 and 3-4-6-4 |
| 3-3-3-4-4 and 3-4-6-4 | 3-3-3-3-3-3 and 3-3-4-3-4 (two) |
The dual tessellations for demi-regular tessellations use more than one tessellating shape. Construct the dual of each of these demi-regular tessellations.
It has been reported by several sources that there are only 14 possible demi-regular tessellations, but an interesting new paper by Ng Lay Ling at http://www.math.nus.edu.sg/aslaksen/projects/nll.pdf disputes this. Thanks to Brian Galebach for pointing this out.
|
All images and text on this page ©2011 by Ephraim Fithian. Email for permission to use any portions. Unauthorized use is a violation of state and federal law. |