Activity 3
The Geoboard
The geoboard is a device used in elementary schools to aid in the
teaching of basic geometric concepts. Geoboards may be purchased
commercially from the usual supply houses or they may be constructed
out of common household materials using common tools. A simple
geoboard can be made from a square piece of wood and 25 finishing
nails. A grid of 5 vertical lines and 5 horizontal lines evenly
spaced are drawn on the square piece of wood. Nails are placed at
the intersections of the lines so that they extend about one
centimeter.
Figures are made on the geoboard by stretching rubber bands from one
nail to another until the desired shape is formed. Segments can be
shown by connecting only two nails. The first task to perform is to
determine how many different segments may be constructed on the
geoboard. As with most of the problem solving situations we will
encounter, we will first simplify the problem, then look for
patterns to help solve it, and then attempt to generalize the
solution. It is easier to work with an actual geoboard than to work
on paper alone, but if a geoboard is not available, dot paper can be
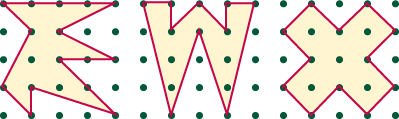
used. The dot paper below shows some figures drawn as if on a
geoboard.
Segments on a Geoboard
Take a geoboard and some rubber bands. Assuming that the shortest
distance between two adjacent nails is one unit, how many segments
could be constructed with a length on one unit? Suppose the
geoboard was a 4 by 4 nail version. Then how many? Find the number
of segments one unit long that can be constructed on a geoboard of
each size given and write the answers in the table.
| Size of Geoboard |
2 by 2 |
3 by 3 |
4 by 4 |
5 by 5 |
6 by 6 |
7 by 7 |
8 by 8 |
9 by 9 |
10 by 10 |
| Number of Segments |
|
|
|
|
|
|
|
|
|
How many segments of this length could you place on an n by
n geoboard? _______
Now make a segment that is as long as the diagonal of a 4-nail
square. How many segments can be constructed with this length? Find
the number of segments of this length that can be constructed on a
geoboard of each size given and write the answers in the table.
| Size of Geoboard |
2 by 2 |
3 by 3 |
4 by 4 |
5 by 5 |
6 by 6 |
7 by 7 |
8 by 8 |
9 by 9 |
10 by 10 |
| Number of Segments |
|
|
|
|
|
|
|
|
|
How many segments of this length can you place on an n by
n geoboard?________
Now make a segment that is as long as the diagonal of a 1 unit by 2
unit rectangle. How many segments can be constructed with this
length? Find the number of segments of this length that can be
constructed on a geoboard of each size given and write the answers
in the table.
| Size of Geoboard |
2 by 2 |
3 by 3 |
4 by 4 |
5 by 5 |
6 by 6 |
7 by 7 |
8 by 8 |
9 by 9 |
10 by 10 |
| Number of Segments |
|
|
|
|
|
|
|
|
|
How many segments of this length can you place on an n by
n geoboard?________
This process can be continued for a segment of any given length on a
geoboard. Use the dot paper below to investigate the solution to
the following generalized problem situation:
How many segments can be constructed on an n by n
geoboard where each segment is the length of a diagonal of a rectangle
a units wide by b units long?__________
Suppose that the rectangle is a square with a units on a
side.________________
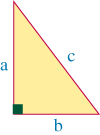
Length of a Segment
The length of any segment connecting
two nails can be found by using the Pythagorean Theorem, which
states that if the two legs of a right triangle have lengths of
a and b respectively, and the hypotenuse has a length of
c, then the following relationship is always true as is shown
in the diagram at the right.
a2 + b
2 = c2
|
|
|
Area of a Figure
|
|
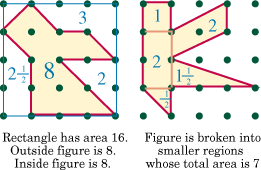
The area of a closed figure on the
geoboard can be found by enclosing the figure with a rectangle,
finding the area of the rectangle, and subtracting the areas of the
portions not in the figure. A second approach to finding the area
of a closed figure is to break the figure into smaller regions whose
areas are easily determined.
|
Construct each of the figures shown below on a geoboard,using rubber
bands to either enclose the figures or to separate the figures into
smaller regions so that the area of each may be easily found. Draw
lines on the figures to show where the rubber bands were placed.
Find the length of each segment in each figure and add these lengths
to find the perimeter of each figure. Write the area and perimeter
below each figure.
| Figure |
 |
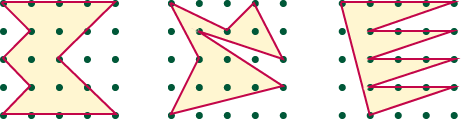| Area |
|
|
|
| Perimeter |
|
|
|
Pick's Formula for Area
It is possible to find the area of a figure made on a geoboard
without using either of the techniques described above. A formula
known as Pick's Formula can be found by examining different
categories of figures and finding their areas. It will be necessary
to count the number of nails inside each figure but not touched by
the figure, as well as the number of nails actually touched by the
figure. We will first examine figures that have exactly one nail
untouched inside the figure. Construct several figures of this
type, count the number of nails touched, and find the area of each
figure, recording your results in the table below. Use this
information to try to guess the formula for n nails touched.
One Nail Inside Figure
| Nails Touched |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
n |
| Area of Figure |
|
|
|
|
|
|
|
|
|
Examine some figures that have no nails untouched inside the figure,
count the number of nails touched, and find the area of each figure,
recording your results in the table below. Guess at any missing
areas and try to guess the formula for n nails touched.
No Nails Inside Figure
| Nails Touched |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
n |
| Area of Figure |
|
|
|
|
|
|
|
|
|
Examine some figures that have exactly two nails untouched inside the
figure, count the number of nails touched, and find the area of each
figure, recording your results in the table below. Guess at any
missing areas and try to guess the formula for n nails
touched.
Two Nails Inside Figure
| Nails Touched |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
n |
| Area of Figure |
|
|
|
|
|
|
|
|
|
Examine some figures that have exactly three nails untouched inside
the figure, count the number of nails touched, and find the area of
each figure, recording your results in the table below. Guess at
any missing areas and try to guess the formula for n nails
touched.
Three Nails Inside Figure
| Nails Touched |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
n |
| Area of Figure |
|
|
|
|
|
|
|
|
|
Use the results of these investigations to complete the following
table with the formulas for the areas when n nails are
touched. Generalize these formulas to the case when k nails are
untouched inside the figure. This generalized formula gives the
area of a figure that touches n nails with k nails
untouched inside the figure and is called Pick's Formula.
k Nails Inside Figure
| Nails Inside Figure |
0 |
1 |
2 |
3 |
4 |
5 |
k |
| Formula for n Nails |
|
|
|
|
|
|
|
Squares on a Geoboard
A fascinating problem on the geoboard is to determine how many
squares can be constructed. It is necessary to consider all
possible sizes and all possible positions. Squares may be made on a
geoboard so that the base of the square either is or is not parallel
to the base of the geoboard. To solve the problem in all its
generality, we need to examine geoboards of different sizes.
A 2 by 2 geoboard can have only one square, and this square is
parallel to the base of the geoboard.
A 3 by 3 geoboard can have 6 squares in all. Five of these squares
are parallel to the base of the geoboard. There are 3 different
squares shown of the 6 possible. The squares are shown on the dot
paper below.
Find all the squares that can be drawn on a 4 by 4 geoboard. Begin
by finding all the different squares that are parallel to the base
and the number of each size. Next, find all the squares that are
not parallel to the base and the number of each. Draw the different
sizes of squares and record the number of each below the dot grid.
Find all the squares that can be drawn on a 5 by 5 geoboard. Begin
by finding all the different squares that are parallel to the base
and the number of each size. Next, find all the squares that are
not parallel to the base and the number of each. Draw the different
sizes of squares and record the number of each below the dot
grid.
Use the results of your investigations to fill in the table below.
Use the patterns in the table to extend the results to 6 by 6, 7 by
7, 8 by 8, 9 by 9, and 10 by 10 geoboards.
The results in the table above can be used to generalize to an n by
n geoboard using the method of Finite Differences. Using
this method, the values for each size are placed in a column next to
a column of different sizes and the differences between consecutive
values are computed. If the differences are not constant, the
second differences are computed, and so on, until the differences
are constant. The formula derived will be a polynomial in n
whose degree will be the order of the differences calculated. The
number of terms will be one more than the order. Therefore the
formula will be of the form
a1nk +
a2nk-1 +
a3nk-2
+ . . . + akn + ak
+1
where k is the order of the differences and n is the
size. The value of a1 is equal to the constant
difference divided by k!.
a1 = constant / k! =
constant / k(k-1)(k-2)...(3)(2)(1)
The example below shows the formula for the total number of squares
on an n by n geoboard that are parallel to the base.
| Size |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
| Squares |
0 |
0 |
1 |
5 |
14 |
30 |
55 |
91 |
140 |
204 |
285 |
| 1st Diff |
0 |
1 |
4 |
9 |
16 |
25 |
36 |
49 |
64 |
81 |
|
| 2nd Diff |
1 |
3 |
5 |
7 |
9 |
11 |
13 |
15 |
17 |
|
Since the third order differences are constant and the value of that
constant is 2, then the formula becomes
1/3 n3 +
bn2 + cn + d
The value of d can be found by replacing n by 0 and
the formula by its value when n is 0, namely 0. The first
three terms are 0; so then, d = 0, and the formula now
becomes
1/3 n3 +
bn2 + cn
The values of b and c can be found by taking two
different values for n and replacing n by these
values in the formula, and solving these two equations
simultaneously.
Solving the two equations simultaneously, it is found that b
= -1/2 and c = 1/6,
giving the final formula as
1/3 n3 -
1/2 n2 + 1/6
n
All images and text on this page ©2011 by Ephraim Fithian.
Email for permission to use any portions.
Unauthorized use is a violation of state and federal law.
|